Mathematical notation on the web – part 1

This article (part 1) is about displaying mathematical notation within web pages and discusses the problems and issues. Part 2 discusses a more recent solution which might appeal to those where mathematics is a core part of their teaching work. If you are already familiar with the background issues to displaying mathematics on the web, then feel free to jump straight to part 2, but if not, you might find it useful to start here.
Part 1 – Problems displaying mathematical notation
Background
Authoring mathematical expressions, equations, and formulas for electronic media such as the web is a problem as old as computers are. Almost as soon as computers had the capability, people started inventing languages to allow them to create printed, typeset mathematical expressions (along with typesetting the text around the expressions). The various languages and formats that make up modern web pages (HTML, XML, CSS, HTML5, etc.) work wonderfully for most purposes, but there is one place where they are still somewhat clunky, namely in the presentation of mathematical equations and diagrams on web pages. While web formats do support very simple mathematical typesetting (such as the usage of basic symbols such as π, or superscripts such as x2), it is difficult to create more sophisticated (and non-ugly) mathematical displays, such as:
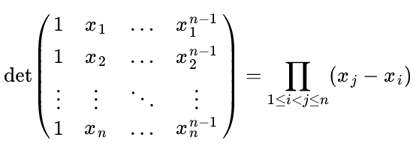
Within the University many staff members often choose to distribute electronic documents containing mathematical notation as either Microsoft Word files or as PDFs. In the former case, Microsoft Word features an in-built equation editor for the authoring of mathematical notation. In the latter case, PDFs can originate from a wide variety of software packages each typically featuring some sort of mathematical authoring solution.
However, when designing content specifically for the web, there are times when it is less desirable to break up the presentation and flow of a web page to take the reader off to a Microsoft application or PDF viewer to view a mathematical document, which is assuming these applications are even installed on the reader’s machine. The web offers many possibilities for delivering rich engaging content – for example, combine a video from a lecture with an interactive 3D representation of a function and embed both in same web page in the context of a textural explanation. But what about if you need to mix some serious mathematics into the document as well?
Technical challenges to working with mathematics in electronic documents
There are many challenges when wanting to get mathematics into an electronic document such as a web page:
- How do I input the mathematical notation?
The natural “interface” for this is a pen and a hard surface, but computers aren’t quite there with this (touch screens may becoming ubiquitous, but the artificial intelligence to recognise and interpret such input isn’t there yet).
Computers work best with a keyboard and mouse. - How does the computer “encode” the mathematical notation?
On the surface, computers are designed to work with alphanumeric characters and a limited range of symbols. Mathematical notation contains a wide range of symbols.
Encoding layout is just as crucial. The position and layout of parts of an equation are just as important as the order of words in a sentence. Get it wrong and the meaning may be completely different or unintelligible. - How does the computer display the mathematical notation back?
Any display of mathematical notation needs to be reliable. But what about accessibility. What if the notation needs to be enlarged on the page or the contrast changed for visually impaired users? Will the quality of the typeset mathematical notation hold? Will that page need to be printable too and how important is the quality of the printed output?
How do I input the mathematical notation?
There are only two real options for this.
- Use a graphical equation editor to build equations from predefined mathematical structural elements (illustrated here). This process is very dependent on the use of the mouse and keyboard. Most people will be familiar with this input method.
- Use a (human readable) mark-up language which has support for mathematics such as LaTeX to input equations as plain text. Clearly input is dependent on the use of the keyboard and knowledge of the mark-up language. LaTeX is a document language for high quality typesetting and is most widely used by mathematicians, scientists, engineers, and other scholars in academia.
Interestingly, in some cases it is possible to have the best of both worlds should you want it – use a graphical editor which simultaneously generates a text-based mark-up equivalent which you can also edit if you know how.
How does the computer “encode” the mathematical notation?
May be we are better first asking “do we even care how the computer encodes the mathematical notation?” Possibly not, especially if we are solely relying on a graphical equation editor for input. It is however worth thinking about how the encoded source of the mathematical input is stored by the computer. Is this locked in a format that is completely dependent on an editor? In the case of a web page, is the encoded source part of the web page itself or separate? These are practical questions worth considering. If the encoded source of the mathematical notation is separate from the output file, but is subsequently lost, you may be forced to author the mathematical notation again from scratch. On the face on it, this feels like a bad idea. It’s better that the encoded source for the mathematical notation travels with the output file. So if we are publishing to the web, the web page we’ve created contains all the information which specifies the symbols and correct layout for the mathematics and can be easily changed there and then.
MathML
The World Wide Web Consortium (W3C), who govern global web standards, recommend a standard called MathML as a means to integrate mathematical formulae into web pages and other documents. The idea behind this being that the structure and content of mathematical notation is encoded using special text markers (XML). Web browsers that support MathML can display this within the web document alongside any other web content (text, images, videos, etc). However, to produce this MathML, a graphical equation editor is almost certainly needed as the syntax of MathML is not particularly human readable. For example, here is a sample of MathML:

…a lot of confusing gobbledygook just to encode the following short equation:
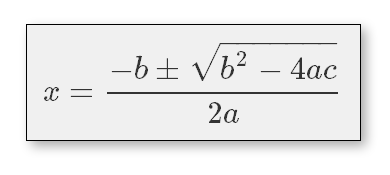
However, as already stated, we may not care about the details of encoding, and instead only care that we have something that works well, and in this case, a W3C recommended format that travels as part of the output web page. Also, many mathematical tools will generate MathML for us.
LaTeX
Alternatively, a very common format for encoding mathematical notation is to use a sub-set of the document language LaTeX (pronounced /ˈleɪtɛk/) which has been around since the early 1980s. LaTeX offers high quality typesetting and is most widely in academia. Typically it is used as an intermediate format to producing document formats such as PDF. LaTeX is not inherently understood by web browsers, but as we shall see later, can be used with the support from an web technology. LaTeX is significantly more human readable than MathML. Compare the following to the previous MathML sample:
x = \frac{-b \pm \sqrt{b^2 – 4ac}} {2a}
…which encodes the same short equation as before:
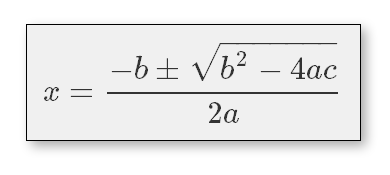
With a little effort, one can make sense of this with sensible guesses and a little logic – \frac means “a fraction” and has two components each wrapped in curly braces { }; \pm means “plus-minus”; \sqrt means “square root” and places everything wrapped in curly braces { } under the square root. More complex examples are obviously harder to follow, but free graphical equation editors are widely available which produce the LaTeX output syntax.
How does the computer display the mathematical notation back?
To date, most approaches for presenting mathematics on the web rely on presenting it back as an image (such as a gif file). This is certainly convenient and ensures that exactly the same is seen across all web browser types and operating systems (Windows, Macs, Linux, etc). However, a dedicated tool still needs to be used to take the mathematical notation and generate the image. So there is a problem with the source used to create the image being separated from the output web page. If any changes to the equation are necessary, we have to go back to the tool that produced the image to make the edits. Secondly, images don’t offer much in the way of accessibly. If the contrast of the page needs to changed or the page background colour for a user with visual impairments, the equation embedded in the image won’t change colour with the page. Thirdly, if the page needs to be printable as well, equations embedded in images tend to lose quality when printed to paper.
MathML offers hope of a better solution, as in theory, all the work in taking the encoded mathematical source and making it display beautiful mathematics is left to the web browser. However, support for MathML amongst web browsers is patchy. The Firefox browser offers good support, but Internet Explorer depends on a special browser plugin. Both the Opera and Chrome web browsers currently offer only limited or no support. This inconsistent browser support is frustrating. However, when MathML is displayed in the Firefox browser it looks very clear and sharp. It also scales well if the page zoom level is increased and prints beautifully.
Finally, there are a range of solutions that use the browser technology Javascript. Javascript is essentially a programming language within the web browser. It is typically used to create enhanced user interactions/interfaces and for the most part you completely take it for granted and are unaware it is being used. Javascript can be used to create a “display engine for mathematics” whereby it takes mathematical notation encoded within the web page (as MathML, LaTeX or simpler notation) and displays the mathematics more or less reliably across all major web browsers.
Finding a good solution
In the next part of this article I shall introduce a modern flexible solution which addresses many of the problems discussed here…

